对抗性样本攻击实验
摘要:根据 PyTorch 官网教程中 Adversarial Example Generation 章节内容,完整实现 Fast Gradient Sign Attack (FGSM) 算法。
题目描述
根据 PyTorch 官网教程中 Adversarial Example Generation 章节内容,完整实现 Fast Gradient Sign Attack (FGSM) 算法。
网址:https://pytorch.org/tutorials/beginner/fgsm_tutorial.html
欺骗模型的方法
本文参考:https://pytorch.org/tutorials/beginner/fgsm_tutorial.html
添加不可察觉对图像的扰动可以导致截然不同的模型性能。
我们将探讨该主题通过图像分类器上的示例。具体来说,我们将使用其中之一第一种也是最流行的攻击方法,快速梯度符号攻击(FGSM),以愚弄 MNIST 分类器。
有许多类别的对抗性攻击,每种攻击都有不同的目标和对攻击者知识的假设。但是,总体而言,首要目标是向输入数据添加最少量的扰动,从而导致所需的错误分类。攻击者的知识有几种假设,其中两种是:白盒和黑匣子。
- 白盒攻击假设攻击者具有对模型的全部了解和访问权限,包括体系结构、输入、输出和权重。
- 黑盒攻击假定攻击者只能访问模型的输入和输出,而对底层体系结构或权重一无所知。
还有几种类型的目标,包括错误分类和源/目标错误分类。
- 错误分类的目标意味着对手只希望输出分类是错误的,但并不关心新分类是什么。
- 源/目标错误分类意味着对手想要更改原始属于特定源类的图像,以便将其分类为特定目标类。
在这种情况下,FGSM 攻击是 白盒 攻击,其目标是错误分类。有了这些背景信息,我们现在就可以详细讨论攻击。
FGSM 快速梯度符号攻击
Fast Gradient Sign Attack (FGSM)
它旨在通过以下方式攻击神经网络:
利用他们的学习方式,梯度。这个想法很简单,而是而不是通过根据反向传播梯度,攻击调整输入数据以最大化基于相同反向传播梯度的损失。换句话说,攻击使用损失的梯度 w.r.t 输入数据,然后调整输入数据以最大化损失。
原理介绍
在我们进入代码之前,让我们看一下著名的 FGSM 熊猫示例 和摘录一些符号。
从图中可以看出,$\mathbf{x}$ 是原始输入图像
正确归类为“熊猫”,$y$是地面真相标签
for $\mathbf{x}$, $\mathbf{\theta}$ 表示模型
参数,$J(\mathbf{\theta}, \mathbf{x},y)$ 是损失
用于训练网络。攻击反向传播
梯度返回输入数据进行计算
$\nabla_{x} J(\mathbf{\theta}, \mathbf{x},y)$.然后,它调整
按一小步输入数据($\epsilon$ 或 $0.007$中的
图片)在方向(即
$sign(\nabla_{x} J(\mathbf{\theta}, \mathbf{x}, y))$)
最大化损失。由此产生的扰动图像$x’$,则
被目标网络错误地分类为“长臂猿”,当它仍然显然是一只“熊猫”。
下面进入实现。
1 | from __future__ import print_function |
FGSM 实现
在本节中,我们将讨论本教程的输入参数,定义受攻击的模型,然后对攻击进行编码并运行一些测试。
本教程只有三个输入,定义为遵循:
- epsilons - 用于运行的 $\epsilon$值的列表。是的
重要的是在列表中保留 0,因为它表示模型
原始测试集上的性能。此外,直观地说,我们会
预期 $\epsilon$越大,扰动越明显
但攻击在退化模型方面越有效
准确性。由于此处的数据范围是 $[0,1]$,因此没有 epsilon
值应超过 1。 - pretrained_model - 通往预训练的 MNIST 模型的路径
- use_cuda - 使用 CUDA 或不使用。
1 | epsilons = [0, .05, .1, .15, .2, .25, .3] |
受攻击的模型
如前所述,受到攻击的模型与来自 pytorch/examples/mnist
您可以训练并保存自己的 MNIST 模型,也可以下载并使用提供的模型。此处的 Net 定义和测试数据加载器具有
是从 MNIST 示例复制的。
本节的目的是定义模型和数据加载器,然后初始化模型并加载预先训练的 weight。
1 | # LeNet 模型定义 |
CUDA Available: True
Net(
(conv1): Conv2d(1, 10, kernel_size=(5, 5), stride=(1, 1))
(conv2): Conv2d(10, 20, kernel_size=(5, 5), stride=(1, 1))
(conv2_drop): Dropout2d(p=0.5, inplace=False)
(fc1): Linear(in_features=320, out_features=50, bias=True)
(fc2): Linear(in_features=50, out_features=10, bias=True)
)
FGSM 攻击函数
现在,我们可以通过以下方式定义创建对抗性示例的函数:
扰动原始输入。fgsm_attack函数需要三个输入,图像是原始干净的图像($x$),epsilon是
像素级扰动量($\epsilon$)和 data_grad
是输入图像的损耗的梯度
($\nabla_{x} J(\mathbf{\theta}, \mathbf{x},y)$).功能
然后创建扰动图像作为
$$
\begin{align}perturbed_image = image + epsilonsign(data_grad) = x + \epsilon sign(\nabla_{x} J(\mathbf{\theta}, \mathbf{x}, y))\end{align}
$$
最后,为了保持数据的原始范围,
扰动图像被裁剪到 $[0,1]$范围内。
1 | # FGSM attack code |
测试攻击效果函数
最后,本教程的核心结果来自test。每次调用此测试函数都会执行一个完整的测试步骤 MNIST 测试集并报告最终精度。但是,请注意此函数还采用 epsilon 输入。这是因为“测试”函数报告受攻击的模型的准确性来自具有实力的对手 $\epsilon$。更具体地说,对于测试集中的每个样本,该函数计算输入数据($data_grad$)的损失会产生扰动带有“fgsm_attack”($perturbed_data$)的图像,然后检查以查看如果令人不安的例子是对抗性的。除了测试模型的精度,该函数还保存并返回一些成功的对抗性示例将在以后可视化。
1 | def test( model, device, test_loader, epsilon): |
实施攻击
实现的最后一部分是实际运行攻击。在这里我们为epsilons输入中的每个 $\epsilon$ 值运行完整的测试步骤。
对于每一个ε,我们还保存了最终的精度和一些成功的结果。在接下来的章节中,我们将列举一些对抗性的例子。注意随着ε值的增加,模型精度降低。而且注意 $\epsilon=0$ 表示原始测试精度,即不进行攻击。
1 | accuracies = [] |
Epsilon: 0 Test Accuracy = 9810 / 10000 = 0.981
Epsilon: 0.05 Test Accuracy = 9426 / 10000 = 0.9426
Epsilon: 0.1 Test Accuracy = 8510 / 10000 = 0.851
Epsilon: 0.15 Test Accuracy = 6826 / 10000 = 0.6826
Epsilon: 0.2 Test Accuracy = 4301 / 10000 = 0.4301
Epsilon: 0.25 Test Accuracy = 2082 / 10000 = 0.2082
Epsilon: 0.3 Test Accuracy = 869 / 10000 = 0.0869
结果分析
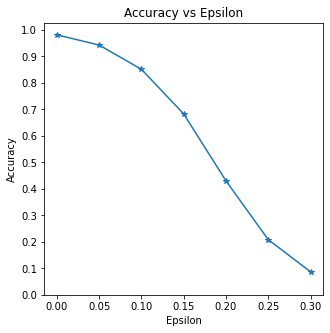
准确性 vs $\epsilon$
第一个结果是准确性与 $\epsilon$ 的关系图。
如前所述,早些时候,随着 $\epsilon$ 的增加,我们预计测试精度会降低。
这是因为更大的 $\epsilon$ 意味着我们在方向将最大化损失。请注意,即使 $\epsilon$ 值是线性间隔的,准确性也不是线性的。
例如,$\epsilon=0.05$时的精度仅低约 4%
大于 $\epsilon=0$,但 $\epsilon=0.2$ 时的准确率为 25%
低于 $\epsilon=0.15$。另外,请注意模型的准确性
达到 10 类分类器的随机精度,介于
$\epsilon=0.25$ 和 $\epsilon=0.3$。
1 | plt.figure(figsize=(5,5)) |
对抗样本实例
还记得没有免费午餐的想法吗?在这种情况下,随着 $\epsilon$ 的增加,测试正确率降低但是扰动变得更加容易感知。
实际上,攻击者必须考虑权衡。在这里,我们在每个 $\epsilon$ 上展示一些成功的对抗示例价值。图的每一行都显示不同的 $\epsilon$ 值。第一个行是 $\epsilon=0$ 示例,表示原始“干净”的图像,无扰动。每个图像的标题显示原始分类 - >对抗性分类。请注意,扰动在 $\epsilon=0.15$ 时开始变得明显,并且很明显在 $\epsilon=0.3$。
然而,在所有情况下,人类都是仍然能够识别正确的类。
1 | # 绘制每个 epsilon 处的对抗性样本的几个示例 |

参考
Adversarial Example Generation — PyTorch Tutorials 1.11.0+cu102 documentation

