Framist's Little House

◇ 自顶而下 - 面向未来 ◇

0%

【MATLAB】多目标优化算法 NSGA-II(gamultiobj) 的使用精解

发表于 更新于 分类于 ，

【MATLAB】多目标优化算法 NSGA-II(gamultiobj) 的使用精解

原始博文因为写的比较潦草，评论中有疑问的网友较多，所以重新写了一下 2021-4-24

增加了一些说明与参考文献，修改了几处笔误 2021-5-20

对于多目标优化（multiobjective optimization）算法 NSGA-II 实现的细节与原理不在此说明。感兴趣的读者可另行查阅

gamultiobj 的使用范式

编写程序

清除所有变量（非必须，但注意变量不能和下面所用的冲突）

1
clear
  • 需求解模型的参数设置部分：（模型导入）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
%% 模型设置
% 适应度函数的函数句柄
fitnessfcn=@Fun;
% 变量个数
nvars=4;
% 约束条件形式1：下限与上限（若无取空数组[]）
% lb<= X <= ub
lb=[0,0,0,0];
ub=[];

% 约束条件形式2：线性不等式约束（若无取空数组[]）
% A*X <= b 
A = [0    0 1 1
    -1/3  0 0 0
     0 -1/2 0 0
     0    0 0 0];

b = [48 ; 30 ; 30 ; 0];

% 约束条件形式3：线性等式约束（若无取空数组[]）
% Aeq*X == beq
Aeq=[1 1 0 0;0 0 0 0; 0 0 0 0; 0 0 0 0];
beq=[120;0;0;0];

目标函数：(这一段需放在脚本最后或单独放在一个文件里)

1
2
3
4
5
6
7
function y=Fun(x)
	% y是目标函数向量。有几个目标函数y就有多少个维度（数组y的长度）
	% 因为gamultiobj是以目标函数分量取极小值为目标，
	% 因此有些取极大值的目标函数注意取相反数
	y(1)=-(x(1)*100/3 + x(3)*90/3  + x(2)*80/2+x(4)*70/2);
	y(2)=x(3)+x(4);
end
  • gamultiobj求解器设置部分：
1
2
3
4
5
6
7
8
%% 求解器设置
% 最优个体系数paretoFraction
% 种群大小populationsize
% 最大进化代数generations
% 停止代数stallGenLimit
% 适应度函数偏差TolFun
% 函数gaplotpareto：绘制Pareto前沿 
options=gaoptimset('paretoFraction',0.3,'populationsize',200,'generations',300,'stallGenLimit',200,'TolFun',1e-10,'PlotFcns',@gaplotpareto);
  • gamultiobj求解与结果输出部分：
1
2
3
4
5
6
7
8
9
10
11
12
%% 主求解
[x,fval]=gamultiobj(fitnessfcn,nvars,A,b,Aeq,beq,lb,ub,options)

%% 结果提取
% 因为gamultiobj是以目标函数分量取极小值为目标，
% 因此在y=Fun(x)里取相反数的目标函数再取相反数画出原始情况
plot(-fval(:,1),fval(:,2),'pr')
xlabel('f_1(x)')
ylabel('f_2(x)')
title('Pareto front')
grid on

RUN

求解时间受求解器设置影响，可能会较长，请耐心等待

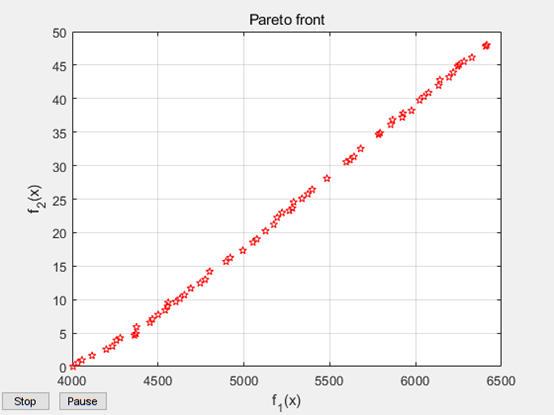
求解过程中会实时显示当前种群的情况：

程序输出

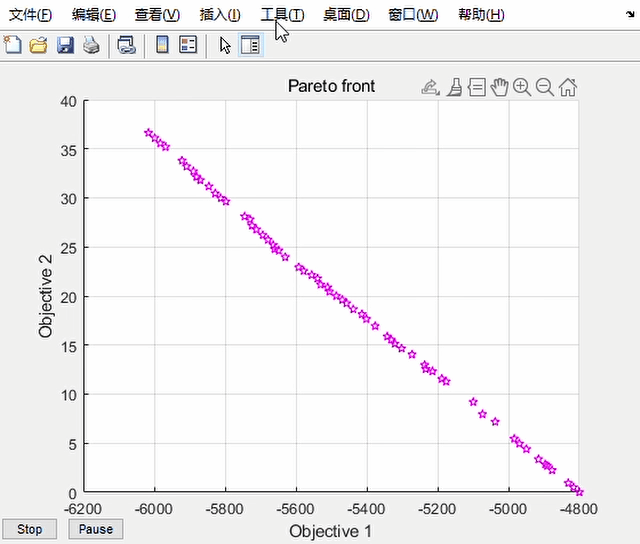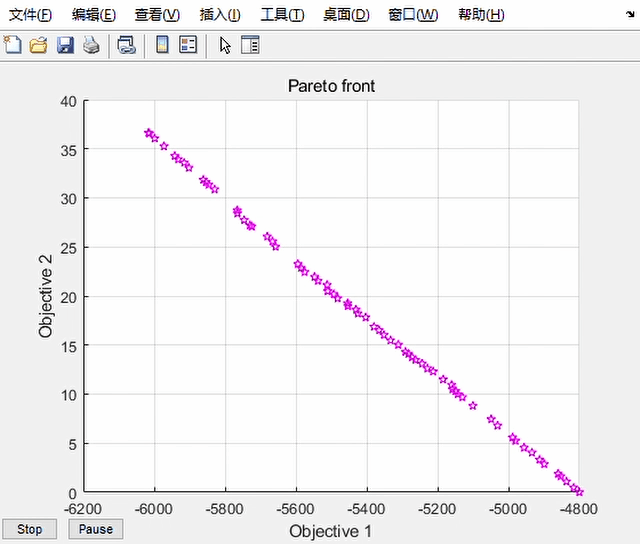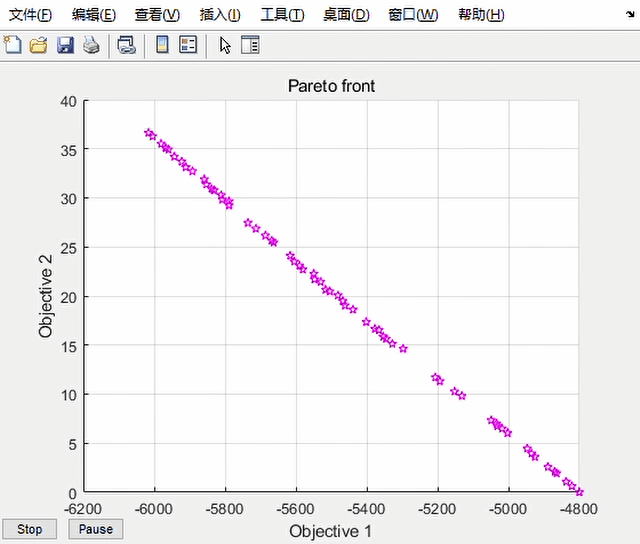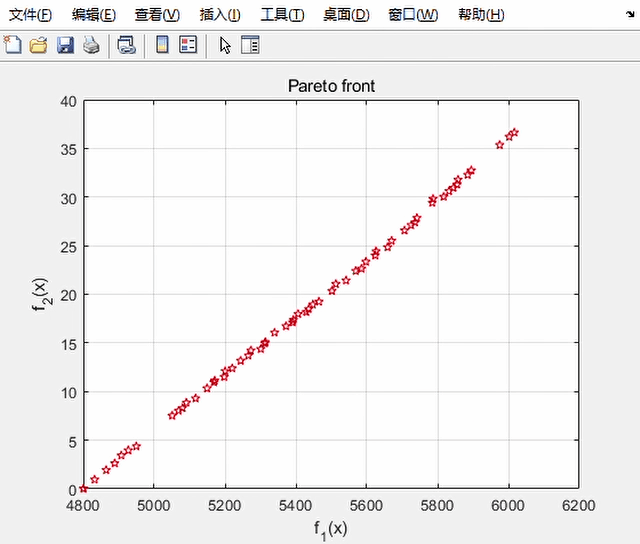
如果已经达到满意，也可点击stop按钮提前结束求解

最后的求解结果，即 Pareto 最优解集储存在[x,fval]中，fval是x对应的目标函数值。fval大致构成了一条空间曲线——Pareto 前沿。若各个解较为均匀分布，说明该图包含了大部分最优解情况，全局性优，适用性强。在满足 Pareto 最优的条件下，是没有办法在不让某一优化目标受损的情况下，令另一方目标获得更优的。所以这些解均为最优，对最优解的具体选择可以根据实际情况。

程序输出

程序输出

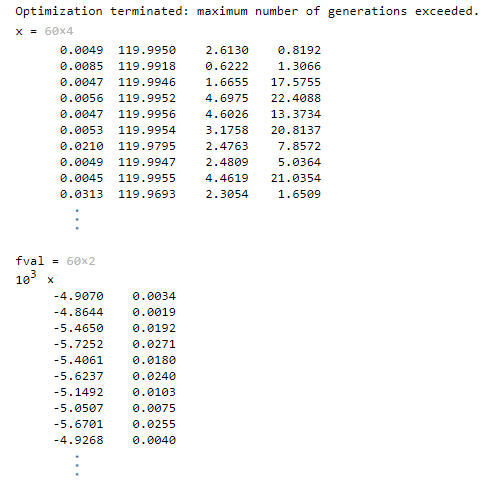
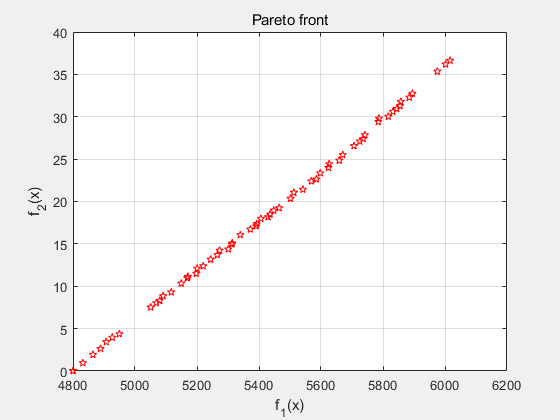
例子 1

Image

表 1 工厂产品生产规格表

产品 生产时间（h/公斤） 利润（元/公斤） 加班时利润（元/公斤）
A 3 100 90
B 2 80 70

设工厂每周生产产品 A、B 的常规生产时长为$x_1$、$x_2$（h），加班生产时长为$x_3$、$x_4$ （h）。令$x=\left( x_1,x_2,x_3,x_4 \right)$ 。设每周的利润函数为$Z(x)$，加班时长函数为$f(x)$。

则目标函数为：
$$
Z\left( x \right) =\frac{x_1}{3}\times 100+\frac{x_3}{3}\times 90+\frac{x_2}{2}\times 80+\frac{x_4}{2}\times 70
$$

$$
f\left( x \right) =x_3+x_4
$$

约束条件为：
$$
\mathrm{s}.\mathrm{t}.\left{ \begin{array}{c}
\begin{array}{c}
\mathrm{x}_1+\mathrm{x}_2=120\
\mathrm{x}_3+\mathrm{x}_4\leqslant 48\
\end{array}\
\frac{\mathrm{x}_1}{3}\geqslant 30\
\frac{\mathrm{x}_2}{2}\geqslant 30\
\mathrm{x}_1,\mathrm{x}_2,\mathrm{x}_3,\mathrm{x}_4\geqslant 0\
\end{array} \right.
$$

因此，数学模型可以归纳为：

$$
min,,F\left( X \right) =\left( -Z\left( x \right) ,f\left( x \right) \right)
$$

$$
\mathrm{s}.\mathrm{t}.\left{ \begin{array}{c}
\begin{array}{c}
\mathrm{x}_1+\mathrm{x}_2=120\
\mathrm{x}_3+\mathrm{x}_4\leqslant 48\
\end{array}\
\frac{\mathrm{x}_1}{3}\geqslant 30\
\frac{\mathrm{x}_2}{2}\geqslant 30\
\mathrm{x}_1,\mathrm{x}_2,\mathrm{x}_3,\mathrm{x}_4\geqslant 0\
\end{array} \right.
$$

MATLAB 求解如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
clear
clc
fitnessfcn=@Fun;
% 变量个数
nvars=4;
% lb<= X <= ub
lb=[0,0,0,0];
ub=[270 240 460 130];
% A*X <= b 
A = [[13 13.5 14 11.5]
    -[13 13.5 14 11.5]
      0 0 -1 0
     [0.015 0.02 0.018 0.011]];

b = [300*48 ; -300*40 ; -150 ; 20];

% Aeq*X = beq
Aeq=[];beq=[];
%最优个体系数paretoFraction
%种群大小populationsize
%最大进化代数generations
%停止代数stallGenLimit
%适应度函数偏差TolFun
%函数gaplotpareto：绘制Pareto前沿 
options=gaoptimset('paretoFraction',0.3,'populationsize',200,'generations',300,'stallGenLimit',200,'TolFun',1e-10,'PlotFcns',@gaplotpareto);

[x,fval]=gamultiobj(fitnessfcn,nvars,A,b,Aeq,beq,lb,ub,options)

plot(-fval(:,1),fval(:,2),'pr')
xlabel('f_1(x)')
ylabel('f_2(x)')
title('Pareto front')
grid on


function y=Fun(x)
	b = [270 240 460 130];
	c = [300 300 600 200];
	t = [190 210 148 100];
	s = [200 230 160 114];
	a = [0.015 0.02 0.018 0.011];
	d = [13 13.5 14 11.5];
	y(1)=-sum(x.*(s-t));
	y(2)=sum(a.*x);
end

得到结果：

Image

x1 x2 x3 x4 如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
119.231391258967	0.769608488165712	0	0

119.231391258967	0.769608488165712	0	0

0.000499510291359209	120.000482867813	13.1757491344817	34.8252467588411

71.3391090591218	48.6614868846125	3.11344686170493	9.36001224382937

…… …… …… ……

27.0549008917871	92.9459248170927	9.47711506311976	25.3969178809142

8.65187243477257	111.349067997015	13.3680683558073	31.7052095195761

例子 2

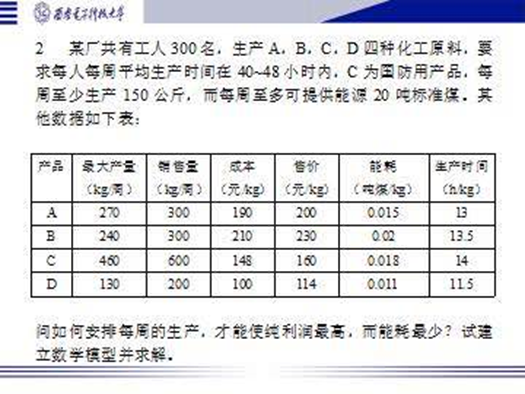
Image

用$\mathrm{i}=1,2,3,4$分别表示 A、B、C、D 四种产品，$x_i$表示第 i 种产品的产量（kg）。设最大产量为$b_i$，销售量为$c_i$，成本为$t_i$，售价为$s_i$，能耗为$a_i$，生产时间为$d_i$。设该问题的利润函数为 $Z\left( x \right)$，能耗函数为$f\left( x \right)$。
则利润函数为：

$$
Z\left( X \right) =\sum_{i=1}^4{x_i\left( s_i-t_i \right)}
$$

能耗函数为：

$$
f\left( x \right) =\sum_{i=1}^4{a_ix_i}
$$

  • 建立模型如下

$$
minF\left( X \right) =\left( -Z\left( x \right) ,f\left( x \right) \right)
$$

$$
\mathrm{s}.\mathrm{t}.\left{ \begin{array}{c}
\begin{array}{c}
x_i\leqslant b_i\left( i=1,2,3,4 \right)\
300\times 40\leqslant \sum_{i=1}^4{x_id_i\leqslant 300\times 48}\
150\leqslant x_3\
\end{array}\
\sum_{i=1}^4{a_ix_i}\leqslant 20\
x_i\geqslant 0\left( i=1,2,3,4 \right)\
\end{array} \right.
$$

  • MATLAB 求解如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
% 清除所有变量（非必须）
clear

%% 模型设置
% 获取目标函数的函数句柄
fitnessfcn=@Fun;
% 变量个数
nvars=4;
% 约束条件形式1：（若无取空数组[]）
% lb<= X <= ub
lb=[0,0,0,0];
ub=[];

% 约束条件形式2：（若无取空数组[]）
% A*X <= b 
A = [0    0 1 1
    -1/3  0 0 0
     0 -1/2 0 0
     0    0 0 0];

b = [48 ; 30 ; 30 ; 0];

% 约束条件形式3：（若无取空数组[]）
% Aeq*X = beq
Aeq=[1 1 0 0;0 0 0 0; 0 0 0 0; 0 0 0 0];
beq=[120;0;0;0];

%% 求解器设置
% 最优个体系数paretoFraction
% 种群大小populationsize
% 最大进化代数generations
% 停止代数stallGenLimit
% 适应度函数偏差TolFun
% 函数gaplotpareto：绘制Pareto前沿 
options=gaoptimset('paretoFraction',0.3,'populationsize',200,'generations',300,'stallGenLimit',200,'TolFun',1e-10,'PlotFcns',@gaplotpareto);

%% 主求解
[x,fval]=gamultiobj(fitnessfcn,nvars,A,b,Aeq,beq,lb,ub,options)

%% 结果提取
% 因为gamultiobj是以目标函数分量取极小值为目标，
% 因此在y=Fun(x)里取相反数的目标函数再取相反数画出原始情况
plot(-fval(:,1),fval(:,2),'pr')
xlabel('f_1(x)')
ylabel('f_2(x)')
title('Pareto front')
grid on


function y=Fun(x)
% y是目标函数向量。有几个目标函数y就有多少个维度（数组y的长度）
% 因为gamultiobj是以目标函数分量取极小值为目标，
% 因此有些取极大值的目标函数注意取相反数
y(1)=-(x(1)*100/3 + x(3)*90/3  + x(2)*80/2+x(4)*70/2);
y(2)=x(3)+x(4);
end

求解结果为：

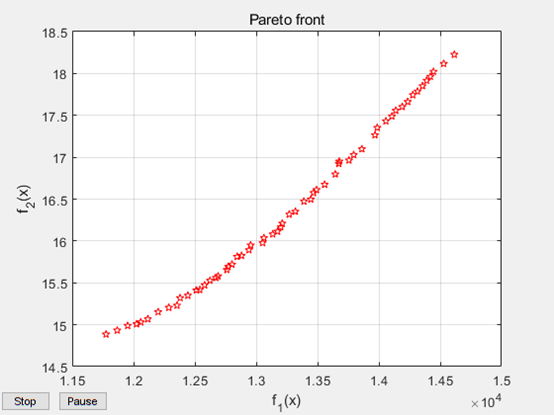
Image

x1 x2 x3 x4 如下：

1
2
3
4
5
6
7
8
9
10
11
257.911499184609	147.920309053797	368.392357989384	129.803238959239

204.527452370415	215.831670926692	376.135110383218	129.541339137201

251.942563886570	239.988410149935	456.713154231118	129.635721179650

…… …… …… ……

245.261897051381	238.784443203755	429.044675830294	129.548264747046

216.531507460989	201.737471951873	368.856283121162	129.726418090506

参考文献：

K. Deb, S. Agrawal, A. Pratap, T. Meyarivan. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002 6(2): 182-197.