【信号与系统 x MATLAB】实验三
实验摘要:
用 MATLAB 进行信号与系统课程第三次实验
主要内容有:
- 图片的高频信息与低频信息(合成、分解图片)
- 频域制作数字盲水印和去除数字盲水印
- 傅里叶变换、傅里叶逆变换与其时移特性
实验题目
- 图片的高频信息与低频信息合成图片。
合成图片。找两张轮廓比较像的图片 A 和 B,有一张是你本人。提取一张照片的低频信息,另一张图片的高频信息,结合这两个照片。设置不同的频率门限,组合照片,组合的效果是,放大看是 A,缩小看是 B。例如以下两张图片
分解图片。把下图爱因斯坦和玛丽莲梦露分开(此图缩小是玛丽莲梦露,截取不同的频段)

频域制作数字盲水印和去除数字盲水印 https://www.zhihu.com/question/50735753,看懂,想想,有想法写出来,做一个好玩的东西。
傅里叶变换两题
使用 2 维离散余弦变换(DCT)分解合成图像的高频和低频
合成图像
分解图像
输出


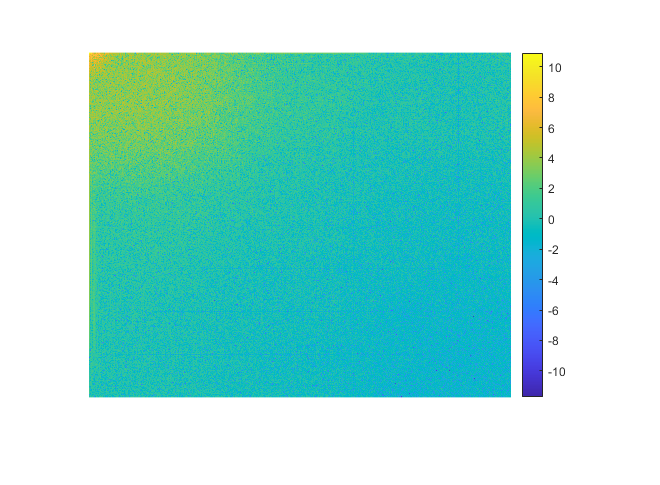

给上一题的图片加上盲水印
输出

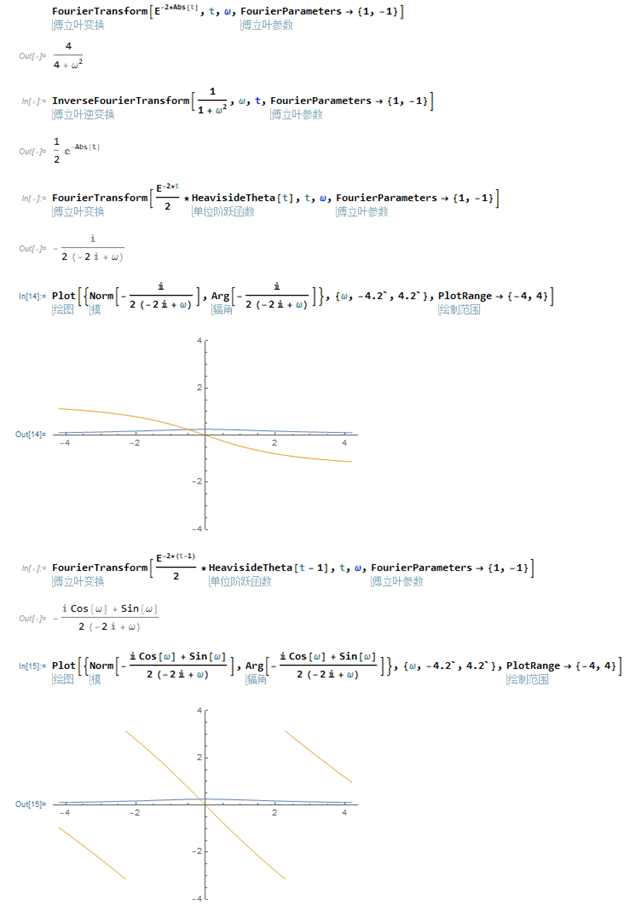
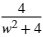
傅里叶变换

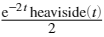
因为涉及到符号计算,于是直接上 Mathematica 写了:
Mathematica 代码:
$\text{FourierTransform}\left[e^{-2 | t| },t,\omega ,\text{FourierParameters}\to {1,-1}\right]$
$\text{InverseFourierTransform}\left[\frac{1}{\omega ^2+1},\omega ,t,\text{FourierParameters}\to {1,-1}\right]$
$\text{FourierTransform}\left[\frac{1}{2} e^{-2 t} \theta (t),t,\omega ,\text{FourierParameters}\to {1,-1}\right]$
$Plot[{Norm[-(I/(2 (-2 I + [Omega])))],
Arg[-(I/(2 (-2 I + [Omega])))]}, {[Omega], -4.2, 4.2},
PlotRange -> {-4, 4}]$
$FourierTransform[E^(-2*(t - 1))/2*HeavisideTheta[t - 1], t, [Omega],
FourierParameters -> {1, -1}]$
$\text{Plot}\left[\left{\left| -\frac{i \cos (\omega )+\sin (\omega )}{2 (-2 i+\omega )}\right| ,\arg \left(-\frac{\sin (\omega )+i \cos (\omega )}{2 (\omega -2 i)}\right)\right},{\omega ,-4.2,4.2},\text{PlotRange}\to {-4,4}\right]$
输出:
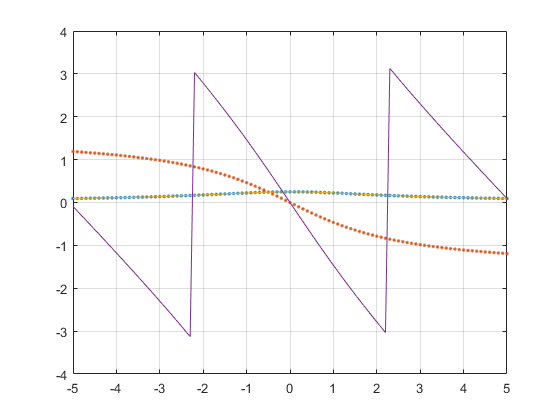
后来有同学问我 MATLAB 怎么写,于是用 MATLAB 又写了一遍(MATLAB 符号计算居然也能用,但依然大大不如 Mathematica)
1 | clear |
部分输出:
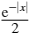


1 | fFwl = 包含以下值的 function_handle: |

1 | fFwl = 包含以下值的 function_handle: |

这个可以看出傅里叶变换的时移特性:能量没变,相位变化了。

